Paint map terrain elevation
128x128 paint map defining the island's base elevation structure

This post is a direct continuation to Part I, where we established the terrain mesh foundation using Poisson disk sampling and Delaunay/Voronoi structures. Now we’ll breathe life into that skeletal framework by assigning elevations to create realistic terrain.

But how do we go from a flat mesh to believable mountains, valleys, and coastlines? The answer lies in carefully layered noise functions, distance fields, and a clever paint map system that ties everything together.

Elevation Color Gradients

Before we delve into elevation itself, we will pick a color gradient to map height values to natural-looking terrain colors. For example, mapgen4 (which inspired this series) uses this color gradient:

Classic elevation gradient
Palette used by mapgen4 - Note the double keypoint around 0.5 to differentiate water/ground
Threshold Color (Hex) Terrain Type
0.0 #1A4D99 Deep ocean
0.495 #80B3E6 Shallow water
0.5 #E6E6E6 Beach sand
0.505 #80CC66 Lowland grass
1.0 #FFFFFF Snow peaks

I will be using this more military-looking palette, though.

Muted elevation gradient
Military-style palette with muted colors for terrain visualization

For proper color blending, the elevation gradients interpolate in linear space rather than directly in sRGB, ensuring smooth transitions without washed out intermediate colors. Not that it matters that much in this particular case, though.

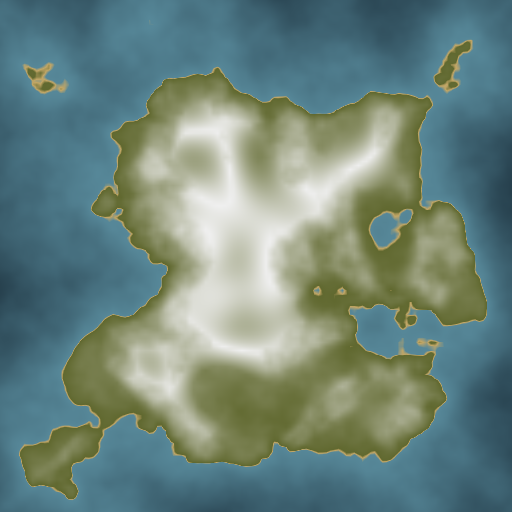
These elevation gradients are used consistently across all elevation-based visualizations in this series: paint maps, triangle elevation, region elevation, and carved terrain. Compared to raw grayscale heightmaps, they provide better visual separation between land and ocean, making the island’s boundaries and topography immediately clear.

The Paint Map Foundation

Let’s start with the foundation: a low resolution paint map that defines the overall island shape. Think of this as the artist’s initial sketch before adding detail. The term “paint map” comes from mapgen4’s interactive feature where users can literally paint elevation changes to sculpt valleys, mountains, and other terrain features.

Whether or not interactive painting is supported, the paint map needs to be initialized with a procedurally generated island shape. This initialization process is our focus in this post.

Paint map showing island shape
Initial paint map with procedurally generated island shape

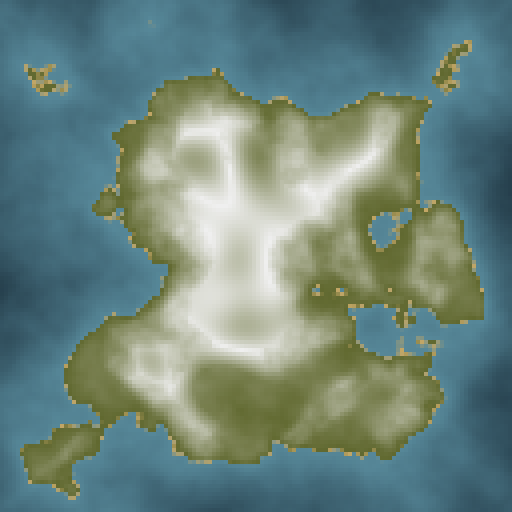
The range of the paint map is remapped to use the color gradient presented above:

  • -1: Deep ocean (dark blue)
  • 0: Sea level (the coastline)
  • +1: Mountain peaks (white)

@redblobgames uses a 128x128 grid in mapgen4, but the actual resolution is not relevant. The idea is to have a coarse approximation to what the island elevation will look like all around. For continent-sized terrains for example you might want to use a larger grid and many more seed points. But for islands like the ones covered in this series, 128x128 will do.

Base Terrain Generation

The foundation of our terrain starts with just two components: a distance-based shape, and fractal Brownian motion (fBm) for organic variation.

Distance field
Distance field (d) - Chebyshev distance from center, creating a square falloff
fBm noise
Fractal Brownian motion (fBm) - Simplex noise (octaves=5, persistence=0.5) for organic terrain variation

These two components are combined according to this base elevation formula:

\[e = \frac{k_{fBm} \cdot \text{fBm} + k_d \cdot (0.75 - 2 \cdot d^2)}{2}\]

This formula creates a pyramid shape (highest at center, lowest at edges) and then adds noise to roughen its surface. Values above zero become land, while values below zero become water.

The specific coefficients and noise functions aren’t critical. Any combination of a distance field and noise will produce island-resembling terrain.

Interactive Parameter Exploration

To understand how the base parameters affect terrain generation, here are animations varying each component:

k_fBm varying from 0 to 1 - Controls the influence of fractal noise
k_d varying from 0 to 1 - Controls the influence of the distance falloff

\(k_{fBm} = 1.0\) and \(k_d = 0.7\) are reasonable defaults.

Mountain Ridges

While distance and fBm create the base terrain, mountain ridges add dramatic peaks and valleys to land areas.

Ridge Pattern Decomposition

Ridge pattern
Ridge pattern (r) - The underlying ridge noise pattern computed globally
Land mask
Land mask (e>0) - Binary mask distinguishing land (white) from water (black)
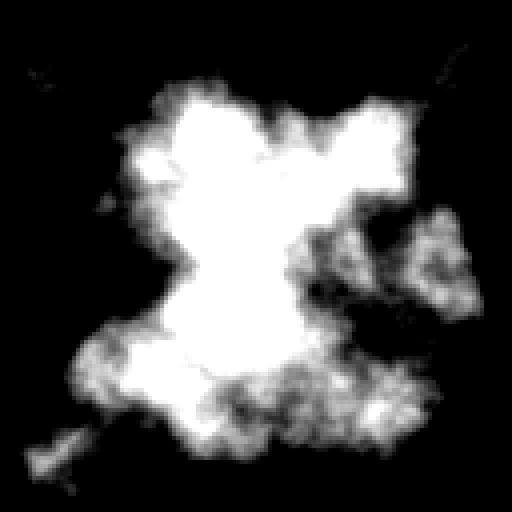
Land strength
Land strength (s) - Elevation-based multiplier (0 for water, up to 1 for peaks)
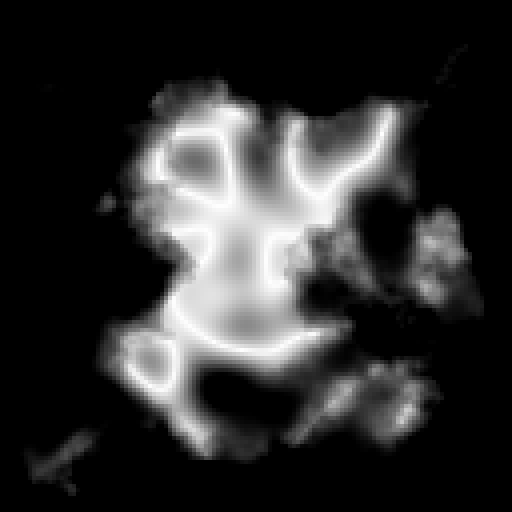
Mountain ridges result
Mountain ridges (m) - Final result: land strength × ridge pattern

The ridge system in mapgen4 works as follows:

\[R = (\text{noise}_1 + \text{noise}_2) \in [-2, 2]\] \[r = \text{saturate}(0, 1 - \lvert R \rvert)\] \[s = \text{saturate}(5e)\] \[r_{final} = \text{clamp}(s \cdot r, e, 3e)\]

The ridge pattern combines two octaves from differently-seeded noise functions. The \(1 - \lvert R \rvert\) transformation creates the characteristic tubular appearance, although any similar function that emphasizes values near zero would work equally well.

The strength multiplier \(s\) ensures ridges fade naturally at coastlines and intensify at higher elevations, confining mountain formation to land areas while scaling with terrain height.

Ridge Influence Animation

Ridge influence varying from 0 to 1: controls how strongly ridges modify the base terrain

Final Composite

Final composite
128x128 paint map - raw visualization
\[e_{final} = e + r_{final}\]

Although the paint map operates at low resolution (128x128), the implementation supports sampling at any floating-point coordinate within the unit square through bilinear interpolation, providing smooth transitions between grid points.

Final bilinear sampled
128x128 paint map - bilinearly sampled in the unit square domain

Next Steps

We’ve established the paint map foundation with fBm noise, island shape constraints, and mountain ridge patterns. This 128x128 grid provides the broad strokes of our terrain. Part III will add the fine details: multi-scale noise layers, distance-based mountain peaks, and elevation blending that brings the terrain to life.

Valuable Resources